Hello World

The problem

Consider the following (simplified) scenario: We have to create a roster composed of three nurses. Each nurse can be assigned to night or day shift, or have the day off. In terms of strict constraints, at least one person needs to take the night shift (by regulation).

Regarding soft or desirable constraints, we know from experience that it is preferable to have two people take the night shift (equality). Moreover one nurse asked us to get the day off and one prefers not to be on night shift but day is fine (noNights). Although, we aim at considering all involved people, the overall organizational constraint equality is deemed more important than the individual wishes. Since we are aiming at a democratic setting, satisfying nurse two’s wish is not comparable to nurse three’s wish. Graphically, we can depict this as follows:

alt text

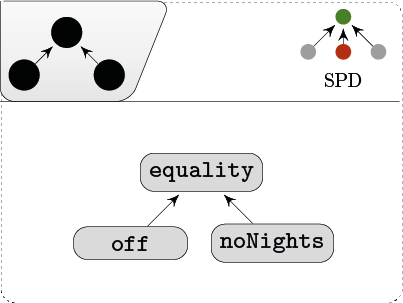
Modeling

We present both the constraint model in MiniZinc and the preference model in MiniBrass for the above problem. If you want to learn more about MiniZinc, have a look at data61’s tutorial.

MiniZinc Model

The MiniZinc constraint model foresees decision variables for every nurse (numbered from 1 to 3). If the solver sets roster[1] = 2 that means that nurse one has to work the night shift.

One hard constraint ensures that at least one nurse is there at night.

include "nurseHelloWorld_o.mzn"; /* the compiled mzn-output */
include "soft_constraints/minibrass.mzn";  /* MiniBrass prepared searches */

/* the actual decision variables and *hard* constraints */
int: day = 1; int: night = 2; int: off = 3;
set of int: SHIFTS = {day, night, off};

set of int: NURSES = 1..3;
array[NURSES] of var SHIFTS: roster;

/* one nurse has to take the night shift */

constraint exists(n in NURSES) (roster[n] = night);

solve search miniBrass();

There are several hooks that connect this hard constraint model with the preference model: include "nurseHelloWorld_o.mzn"; /* the compiled mzn-output */ includes the generated code that results from compiling the (following) preference model into MiniZinc.

The solve item refers to search miniBrass(); which is a MiniSearch search annotation that executes branch-and-bound search, by default. Not that there is no output item as we write it in the preference model – for technical reasons.

MiniBrass Model

Now it is time to state our actual preferences in the MiniBrass model! To capture the above relational (comparative) view, we employ the type ConstraintPreferences that allows us to denote a partially-ordered importance relation over soft constraints.

include "defs.mbr";

PVS: cp1 = new ConstraintPreferences("cp1") {
  soft-constraint equality: 'sum(i in NURSES)(roster[i] = night) = 2';
  soft-constraint noNight: 'roster[2] in {day, off}';
  soft-constraint off: 'roster[3] = off';
  crEdges : '[| mbr.noNight, mbr.equality | mbr.off, mbr.equality |]';
  useSPD: 'true' ;
};

output '["roster = \(roster);"]' ;

solve cp1;

The type ConstraintPreferences (imported from the MiniBrass standard library defs.mbr) expects boolean expressions as soft constraints as well as a graph denoting importance (crEdges). Setting mbr.noNight, mbr.equality makes an edge from the soft constraint noNight to equality. Hence noNight (nurse two’s wish) is less important than equality and similarly for off. The prefix mbr. indicates a keyword that MiniBrass needs to parse. Otherwise, code in single quotes is interpreted as verbatim MiniZinc code – as can be seen in the output item.

We have to compile the preference model using the command:

java -jar mbr2mzn.jar nurseHelloWorld.mbr

or, if you have the MiniBrass directory in your path environment variable,

mbr2mzn nurseHelloWorld.mbr

This command will output (by default) to nurseHelloWorld_o.mzn, the file which is included by the above constraint model. You can change this by setting the -o option of mbr2mzn

Inspecting the results

The selected search strategy solve search miniBrass(); leads to branch-and-bound search where each found solution triggers a new constraint that asks the subsequent solution to be better. We investigate a possible stream of solutions:

Intermediate solution:roster = [2, 1, 1];
Valuations: mbr_overall_cp1 = {1,3}
----------
Intermediate solution:roster = [2, 2, 1];
Valuations: mbr_overall_cp1 = 2..3
----------
Intermediate solution:roster = [2, 1, 2];
Valuations: mbr_overall_cp1 = 3..3
----------
==========

The first solution, [2, 1, 1], is interpreted as nurse one taking the night shift and nurse two and three having the day shift. That only satisfies the second soft-constraint, noNight. This results in the violation set {1,3}, meaning that the first and third soft constraint are violated.

The next solution, [2, 2, 1], is better than [2, 1, 1] since it “trades” the violation of soft constraint equality (number 1) present in [2, 1, 1] for a violation of the second soft constraint (nurse two has to take the night shift). However, now we have two nurses on night shift which satisfies the equality soft constraint.

Finally, [2, 1, 2] puts nurses one and three on night shift, leaving nurse two to her day off. Compared to [2, 2, 1], we violate one less constraint. We cannot get rid of violating constraint off without any expenses, so we accept [2, 1, 2] as an optimal solution.

However, this clearly is only one optimal solution. Had we found [2, 2, 3] before, nurse two would have to swallow the bitter pill and take the night shift to make nurse three happy. Both [2, 1, 2] and [2, 2, 3] are incomparably optimal but instances of frequently occurring real-life decision situations.

MiniBrass aims at making such situations more transparent than a plain utility value, a single number.

Source code

The source code for this hello-world example can be found at https://github.com/isse-augsburg/minibrass/tree/master/example-problems/nurse-example.

Improve this page

Getting Started

Language Reference